Ideałem byłoby złożenie w wyobraźni siatki w sześcian, ale bądźmy realistami - nie potrafi tego nawet bardzo wielu dorosłych. Może więc jakaś prosta reguła? Najlepiej już teraz powiedzmy „głośno i wyraźnie”:
NIE MA magicznego sposobu, który pozwoliłby rozpoznać prawidłową siatkę sześcianu „od pierwszego wejrzenia”!
Nie ma cudownej reguły, ale są w miarę proste zasady, które pozwolą dosyć szybko ocenić czy z danej siatki wyjdzie sześcian (poniżej będą omówione i wyjaśnione). Powiedzmy jeszcze w tym miejscu o dwóch sposobach, które pozwalają z jednej siatki otrzymywać pozostałe - po lewej fragment artykułu Marka Kordosa z „Małej Delty” (1992 r.), w którym nowe siatki otrzymuje się przez obrót ścian dokoła wierzchołków (link), a po prawej jedna z układanek, gdzie najpierw na sześcianie numeruje się wszystkie krawędzie na obu sąsiadujących ścianach, a później wycina się ściany i układa jak kostki domina tworząc nowe siatki.
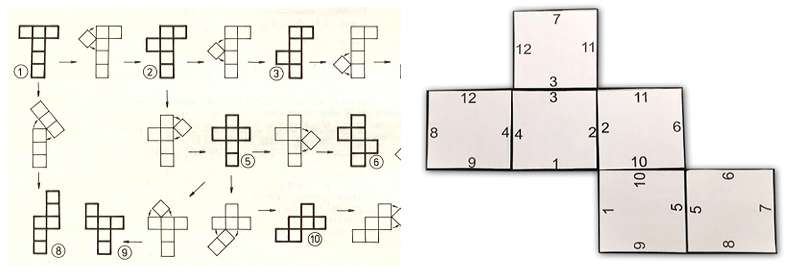
Oba te sposoby nie nadają się do zastosowania na „kartkówkowym lub egzaminacyjnym froncie” - pierwszy jest czasochłonny, trudny i zbyt akademicki, zaś drugi to zabawa klockami, które trzeba przede wszystkim mieć pod ręką.
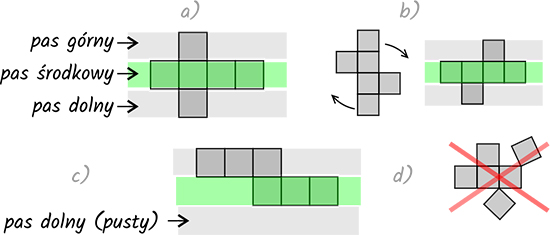
Przyjmujemy, że wszystkie nasze siatki będą ułożone poziomo (wyraźna tendencja w zadaniach matematycznych o siatkach) i będą leżeć w trzech pasach (rysunek a)).
Jeśli mamy siatkę w pionie, to możemy obrócić kartkę (b)).
Jeśli siatka zajmuje tylko dwa pasy, to oznacza, że trzeci jest pusty (c) - jest tylko jedna taka siatka).
Dla przyzwoitości przypomnijmy również, że w siatce ściany muszą być styczne krawędziami, więc nie może być sytuacji pokazanej na rysunku d).
Siatka NIE MOŻE składać się z jednego pasa sześciu ścian!
Animacja wyjaśnia dlaczego - po zawinięciu siatki dwie ściany zostają bez przydziału, a dwie ściany są puste.

Z tych samych powodów NIE MOŻE istnieć siatka mająca w pasie pięć kwadratów - tutaj też jedna ściana zostanie pusta.

NIE MOŻE istnieć siatka mająca 4 kwadraty ułożone w kwadrat.
W animacji widać, jak jeden z kwadratów zawsze wtedy trafi na już zajęte miejsce.

NIE MOŻE istnieć siatka, w której pomiędzy dwoma kwadratami w tym samym pasie jest przerwa - jeden z nich zawsze wtedy trafi na już zajęte miejsce, a jedna ze ścian zostanie pusta.

NIE MOŻE istnieć siatka, która mając 4 kwadraty w jednym pasie, pozostałe dwa ma obok siebie w innym pasie - wtedy też jedna ze ścian trafi na już zajęte miejsce.

To były wszystkie sytuacje, które nie mogą pojawić się w siatkach, gdyż wtedy nie powstanie z nich sześcian. Poniżej przegląd sytuacji możliwych, w których nadal trzymamy się zasady poziomego położenia siatki rozłożonej w trzech poziomych pasach.
Z ostatniej animacji wiemy już, że przy 4 kwadratach w jednym, środkowym pasie, pozostałe dwa nie mogą być obok siebie - musimy je podzielić po jednym na pas górny i dolny.
Rysunki po prawej pokazują jak zostawiając jeden w tym samym miejscu (czerwony kwadrat), drugi możemy przesuwać dostawiając do kolejnych ścian siatki.
W ten sposób otrzymamy 6 różnych siatek - wszystkie pozostałe (na rysunku blade i półprzezroczyste) to odbicia symetryczne tych sześciu.
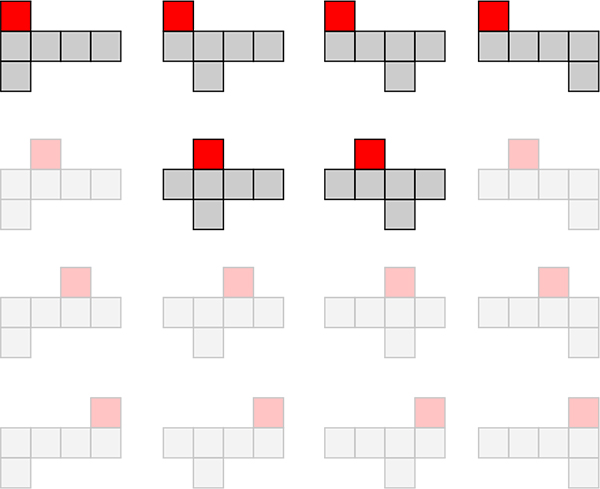
Oto 4 różne siatki sześcianu przy trzech kwadratach w pasku środkowym.
Jest ich jeszcze kilka, ale podobnie jak wyżej, to tylko symetryczne odbicia tych czterech unikalnych siatek.

W tym przypadku jest tylko 1 unikalna siatka sześcianu (w każdym poziomym pasie po 2 kwadraty obok siebie).

Wszystkie 11 różnych siatek sześcianu razem (kolejno po 4, 3 i 2 kwadraty w środkowym pasie).
Obejrzyj 11 animacji 3D pokazujących, jak powstają z tych siatek sześciany. (LINK)

Sprawdźmy na gorąco Twoje rozpoznawanie siatek sześcianu (natychmiastowe odpowiedzi).