Przypomnijmy treść zadania: Wierzchołek D rombu ABCD leży na symetralnych boków AB i BC. Oblicz miary kątów tego rombu.
Zadanie jest zapożyczone z podstawy programowej z matematyki (2025/26). Poniżej podajemy dwa rozwiązania tego zadania - klasyczne, które występuje w chyba wszystkich jego rozwiązaniach (dla szkoły podstawowej) i drugi sposób, w którym pojawia się krótki rachunek.
Sposób klasyczny
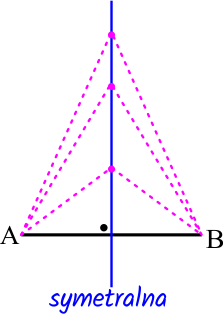Dla przypomnienia: symetralna odcinka to zbiór punktów równo odległych od jego końców. W efekcie otrzymujemy prostą zawsze prostopadłą do odcinka i przecinającą go w połowie (rysunek po prawej).
W rozwiązaniu korzysta się z porównywania lewych i prawych stron równości, czyli tak:
jeżeli x = y ale też y = z, to oznacza, że x = z.
Przykład: jeśli Ania ma taki sam wzrost jak Janek, a Janek ma taki sam wzrost jak Zosia, to znaczy, że Ania i Zosia też mają taki sam wzrost.
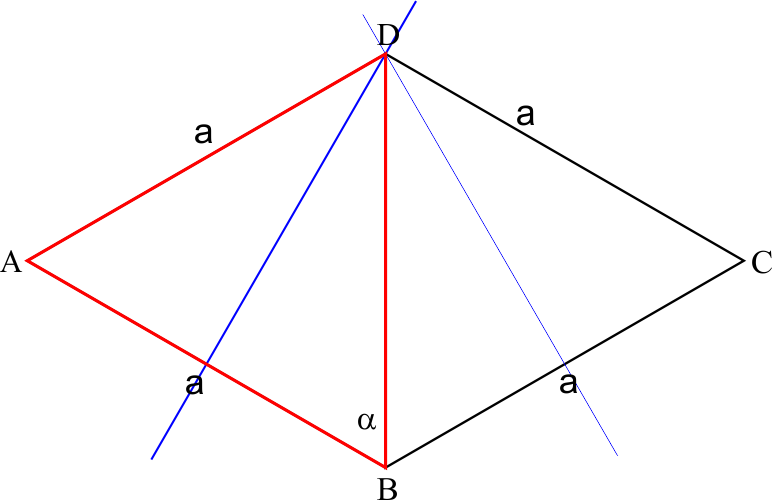Mamy więc romb i symetralne boków AB i BC - wykorzystajmy symetralną AB i trójkąt ABD.
Długość odcinków zapisuje się z pionowymi kreskami (np. |AB| ) - dla czytelności zapisu będziemy pisać długości bez tych kresek.
Z własności symetralnej mamy: BD = AD (odcinki z symetralnej do końców odcinka są równe)
ale z własności rombu mamy też: AD = AB (boki rombu są równe).
To oznacza, że BD = AB, czyli wszystkie te odcinki są równe - trójkąt ABD jest równoboczny (kąty wewnątrz po 60°).
Wyjaśnijmy to jeszcze raz:
odcinek BD (Ania z naszego przykładu) = odcinek AD (Janek), ale AD (Janek) = AB (Zosia), co oznacza, że BD (Ania) = AB (Zosia) (wszyscy mają ten sam wzrost).
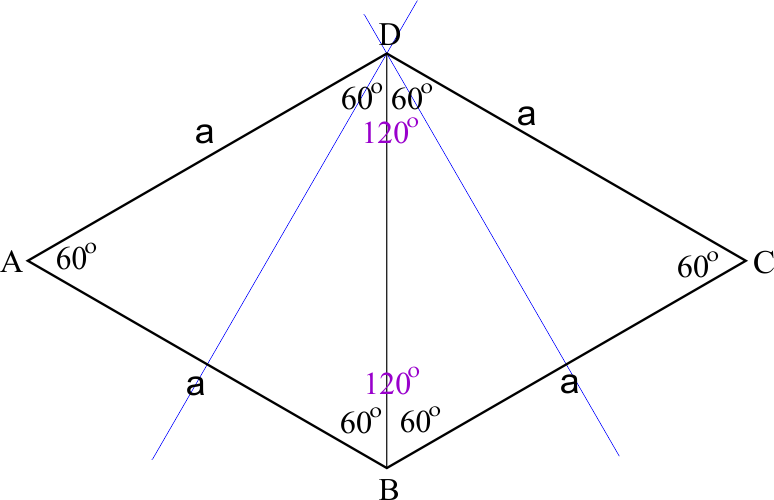Po "drugiej stronie rombu" jest tak samo, więc możemy już odpowiedzieć na pytanie z zadania:
Odp. Kąty takiego rombu mają po 60° i 120°.
W rozwiązaniu wykorzystano ten sa odcinek (u nas AD) jako "łącznik" pomiędzy własnościami symetralnej i własnościami rombu. Drugi sposób opiera się na innym założeniu - przyglądamy się odcinkom AB i BC wraz z ich symetralnymi, bez początkowego myślenia, że to część rombu.
II sposób
W tym sposobie posłużymy się symulacją (poniżej) - mamy dwa równe odcinki (AB i BC) wraz ze swoimi symetralnymi, a kąt między nimi (α) zmienia się, co powoduje, że punkt D wędruje sobie w pionie, tworząc bez przerwy różne czworokąty ABCD.
Możesz zatrzymać symulację i użyć suwaka, a potem strzałek z klawiatury aby badać zmiany "krok po kroku".
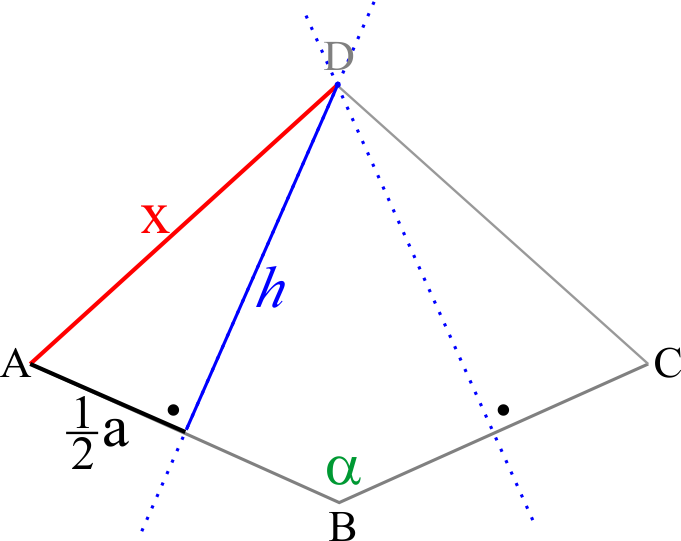W czasie symulacji mamy ciągle pewien trójkąt prostokątny - połowa odcinka AB (u nas oznaczona
1⁄2 a), zmieniające się niebieskie h (to fragment symetralnej, więc wiemy, że trójkąt jest prostokątny) i również nieustannie zmienny czerwony odcinek x (czyli AD).
Trójkąt jest prostokątny, więc ułóżmy dla niego ogólne równanie wynikające z tw. Pitagorasa:
\[ (\frac{1}{2}a)^2 + h^2 = x^2 \]
czyli \( \frac{1}{4}a^2 + h^2 = x^2 \)
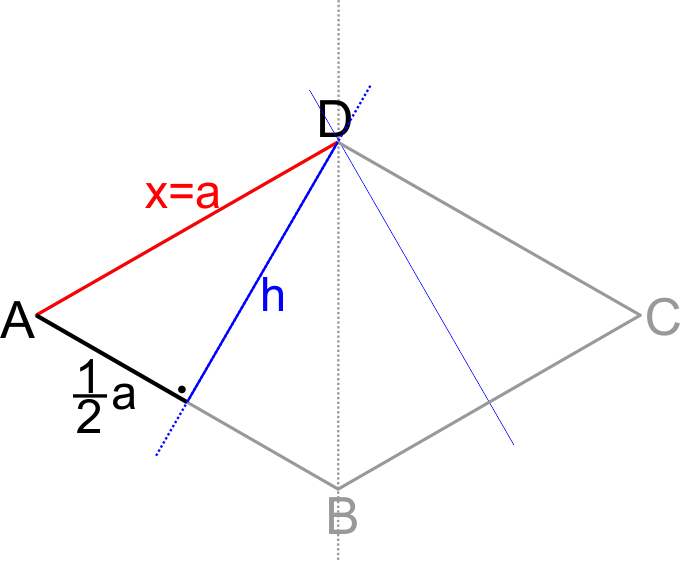Jest taki moment w symulacji, w którym odcinek x będzie miał taką samą długość jak AB, czyli powstanie wtedy romb. Podstawmy w naszym równaniu za x bok rombu (a) i wyliczmy z niego wysokość h:
\[ \frac{1}{4}a^2 + h^2 = a^2 \]
Wyliczamy z tego równania wysokość h:
\[h^2 = a^2 - \frac{1}{4}a^2 \]
\[h^2 = \frac{3}{4}a^2 \]
\[h = \sqrt {\frac{3}{4}a^2} \]
\[h = \frac{\sqrt{3}}{2}a \]
I wszystko jasne! "Każdy" ósmoklasista od razu kojarzy ten wzór - to przecież wysokość trójkąta równobocznego. A jeśli trójkąt ABD jest równoboczny, to kąty w nim mają po 60°, a w całym rombie po 60° i 120°.
