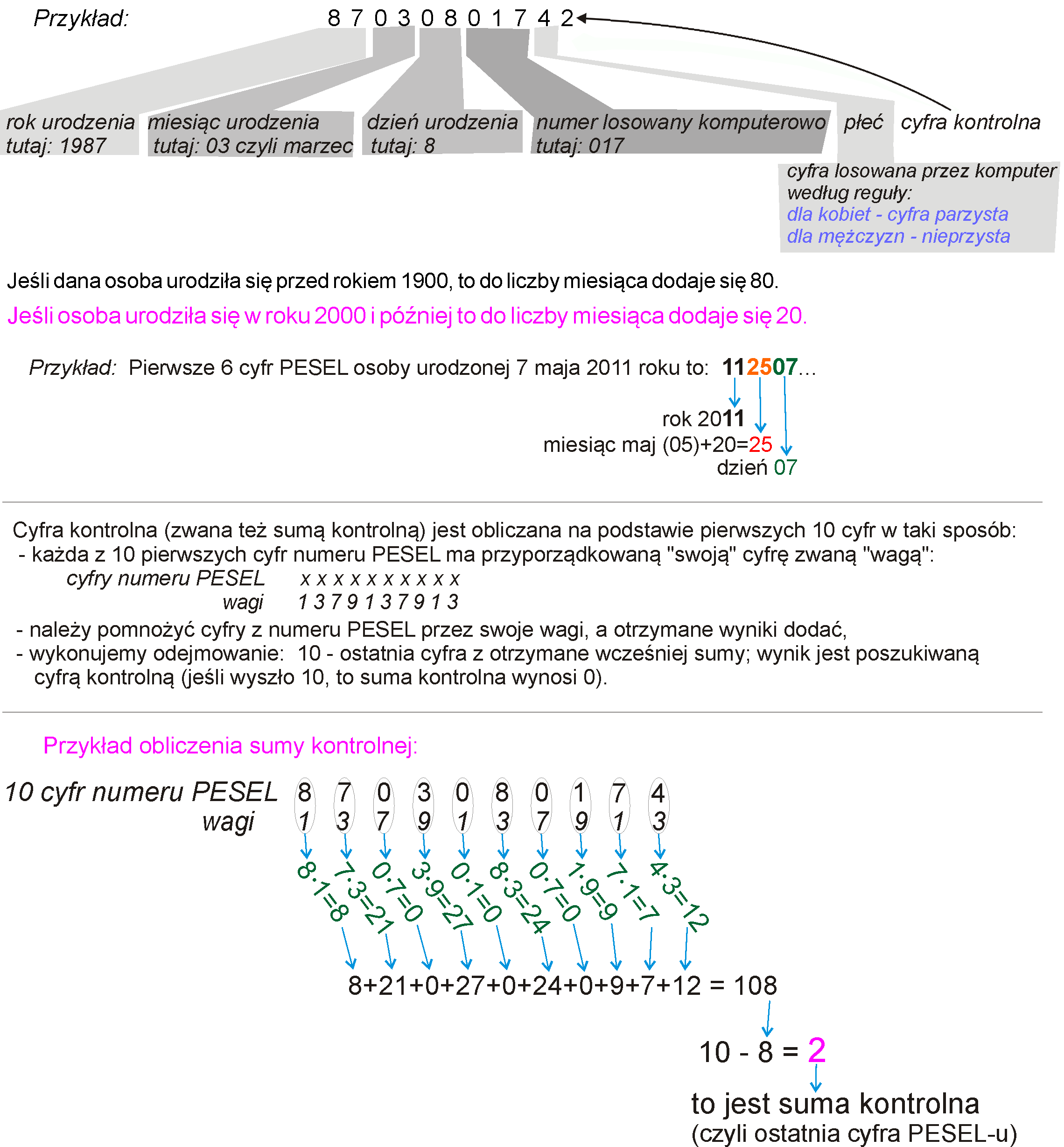
Napisz program, który po wprowadzeniu pierwszych 10 cyfr PESEL obliczy ostatnią cyfrę kontrolną.
Do rozwiązania tego zadania może posłużyć arkusz kalkulacyjny lub jakiś język programowania.
Poniżej "kluczowe" wskazówki dotyczące takiego programu w arkuszu kalkulacyjnym i w języku Python.
Dowolny arkusz kalkulacyjny
Zdecydowanie najławiej jest stworzyć taki program w arkuszu kalkulacyjnym, gdzie każdą cyfrę PESEL-u możemy wpisywać w osobną komórkę, pod nimi wagi, a np. jeszcze niżej wyniki mnożenia cyfr przez wagi i gdzieś w osobnej komórce sumę tych iloczynów.
Komórki z obliczeniami można ukryć (dla estetyki).

Jest to klasyczna tematyka w nauce o arkuszu kalkulacyjnym i jedyna trudność pojawia się przy "wyciągnięciu" ostatniej cyfry z sumy (aby odjąć ją od 10 i otrzymać szukaną cyfrę kontrolną).
Rozwiązaniem jest wykorzystanie dzielenia modulo, czyli dzielenia, w którym nie interesuje nas wynik, a reszta. Jeśli więc otrzymamy sumę np. 67, to aby "wyciągnąć" ostatnią cyfrę (7) musimy podzielić 67 przez 10 (wynik 6 reszta 7) i zabrać właśnie resztę - tak działa dzielenie modulo, a jego formuła to: = MOD(67;10)
Program w języku Python
W prostszej wersji takiego programu można wprowadzać każdą cyfrę PESEL osobno i od razu mnożyć ją przez wagi, iloczyny dodać i ... dojść do tego samego problemu jak w arkuszu - jak "wyciągnąć" ostatnią cyfrę sumy?
Tutaj również przyda się dzielenie modulo, które w Pythonie ma znak % (procentu): ostatniacyfra=suma%10
Co jeśli chcielibyśmy wprowadzić w programie możliwość podania PESEL-u w jednym ciągu cyfr?
Możliwości rozwiązań jest kilka, ale pamiętajmy, że szukamy rozwiązania zrozumiałego dla osoby początkującej w programowaniu, dlatego też można ponownie wykorzystać "cichego bohatera" tego problemu, czyli dzielenie modulo.
10 początkowych cyfr PESEL-u traktujemy jak "pełną" liczbę, czyli np. 8002050123 to 8 mld 2 mln 50 tys. 123.
Jak "wyciągnąć" pierwszą cyfrę? Trzeba podzielić całą liczbę przez 1 miliard i zabrać tylko część całkowitą (w Pythonie to int
cyfra_1 = int(liczba/1000000000)
Teraz druga cyfra - trzeba podzielić liczbę przez 100 milionów (o jedno zero mniej niż wcześniej), zabrać tylko część całkowitą (otrzymamy liczbę dwucyfrową), a następnie podzielić modulo 10.
cyfra_2 = int(liczba/100000000)
Cyfra trzecia - trzeba podzielić liczbę przez 10 milionów (o jedno zero mniej niż wcześniej), zabrać tylko część całkowitą (otrzymamy liczbę trzycyfrową), a następnie podzielić modulo 10.
cyfra_3 = int(liczba/10000000)
itd.
Cyfrę dziesiątą otrzymujemy prościej:
cyfra_10 = liczba%10
Później już "normalnie" - cyfry pomnożyć przez wagi, dodać wyniki, itd.