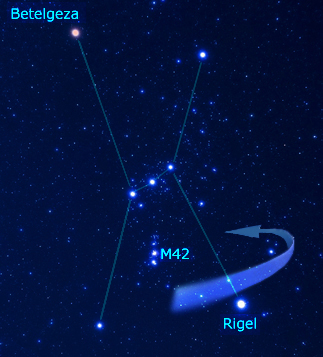
Bohaterem tego tematu jest Orion - jeden z najbardziej charakterystycznych gwiazdozbiorów zimowego nieba. Pierwsze co widać to cztery gwiazdy narożne i Pas Oriona - trzy gwiazdy w środku, leżące "w jednej linii". W "narożnikach" są jedne z najjaśniejszych gwiazd nieba - Rigel, i lekko czerwonawa Betelgeza, która "wkrótce" wybuchnie jako supernowa stając się widoczną w dzień (spokojnie, nic nam nie grozi). Poniżej pasa Oriona widać grupę gwiazd, a wśród nich rozmytą plamkę - to Wielka Mgławica w Orionie (M42).
Orion jest jednym z około 20 gwiazdozbiorów, które widać tak z półkuli północnej jak i południowej, co okazuje się niezwykle ważne dla naszej dalszej opowieści.
Zobacz przy okazji jak wygląda Orion z boku i jakie są odległości do pokazanych gwiazd - LINK
Cóż więc takiego się stanie, gdy przyzwyczajeni do widoku nieba nad Polską, pierwszy raz spojrzymy na nie z półkuli południowej, np. z Australii?
Na pierwszy rzut oka wszystko wydaje się takie samo - narożne gwiazdy, trzy środkowe w linii "idą w prawo do góry" . . . . Na drugi rzut wydaje nam się, że coś "tu jednak nie gra". Dopiero "po chwili" orientujemy się, że mgławica M42, która widziana z Polski jest pod Pasem Oriona, tutaj jest nad nim. Dalsze przyglądanie się ujawnia kolejne niezgodności i jest już pewne, że Orion wygląda "inaczej" niż widziany z Polski.
To jest zawsze duże zaskoczenie, gdyż "nikt o tym wcześniej nie mówił". Po wpisaniu w wyszukiwarce hasła "wygląd tych samych gwiazdozbiorów z półkuli północnej i południowej", w żadnej z wielu pierwszych wyświetlonych stron nie napisano, że ich wygląd będzie się różnił, a najpopularniejsza platforma sztucznej inteligencji podaje o całym zjawisku mętne lub fałszywe informacje!
Wyjaśnienie, dlaczego te same gwiazdozbiory oglądane z półkuli południowej wygladają "inaczej", choć jest teoretycznie proste, to dla bardzo wielu osób (w tym uczniów) sprawia kłopot z powodu konieczności operowania wyobraźnią w trójwymiarowym świecie Ziemi i kosmosu. Dlatego też podamy aż trzy przykłady próbujące zilustrować ten problem.
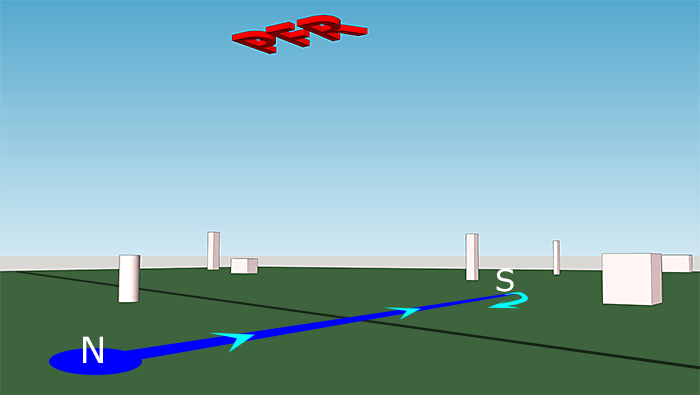
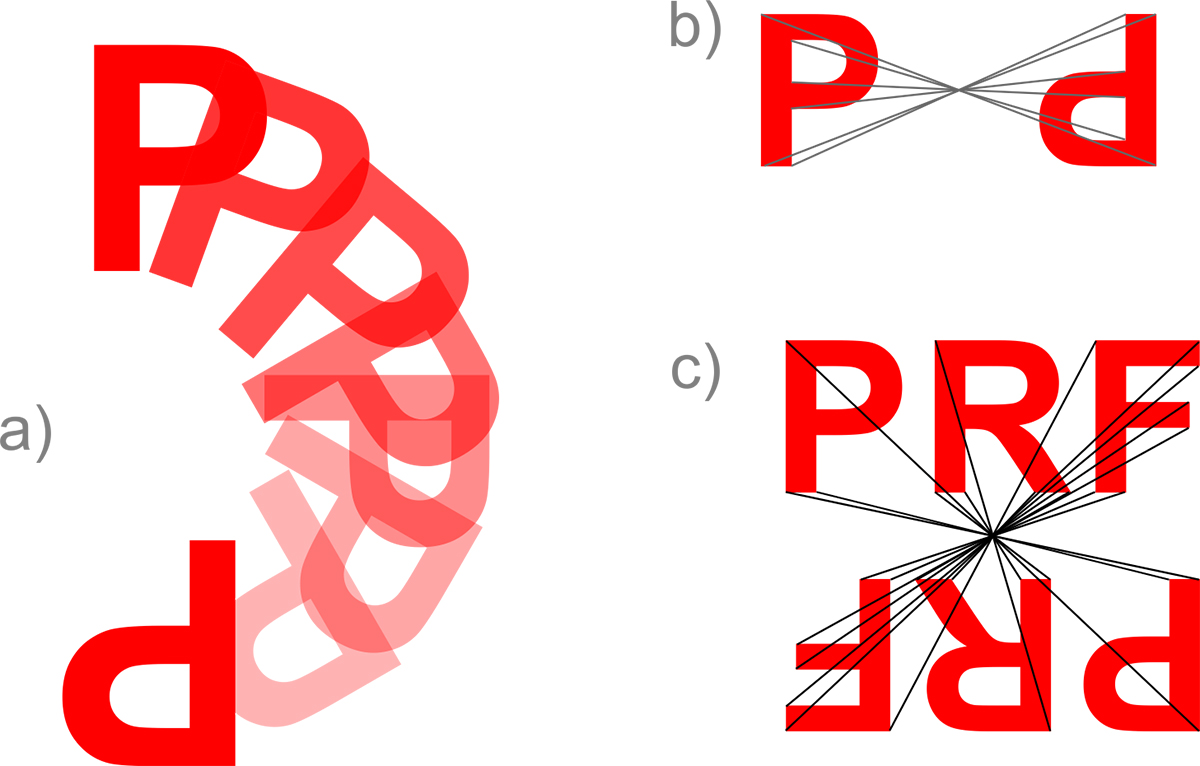
W zasadzie już ten pierwszy wyjaśnia istotę: przechodzimy z punktu N do S pod napisem "PFR", po czym obracamy się o 180°. Dlaczego "PFR"? Bo te litery nie mają wewnętrznej symetrii i dobrze nadają się do ilustracji wszelkich przekształceń.
Filmik pokazuje jak będą wyglądały litery "PFR" po obróceniu się w punkcie S - są "do góry nogami" i zmieniła sie ich kolejność.
Ta sama historia, ale w otoczeniu Ziemi. Przemieszczamy się z półkuli północnej na południową pod napisem "RFL", a na końcu odwracamy się o 180°.
Mamy to samo co wcześniej - napis jest "do góry nogami", a np. litera R z pierwszej w napisie przeszła na ostatnią.
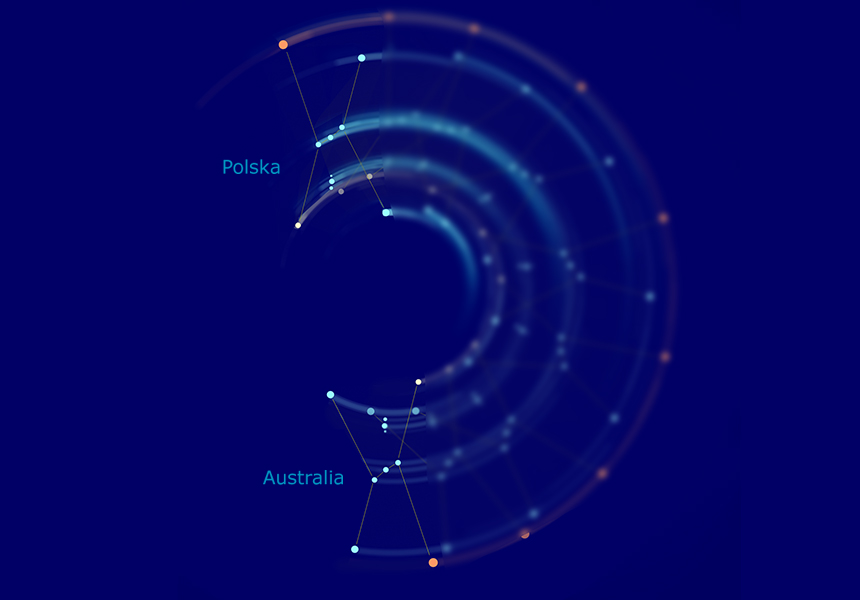
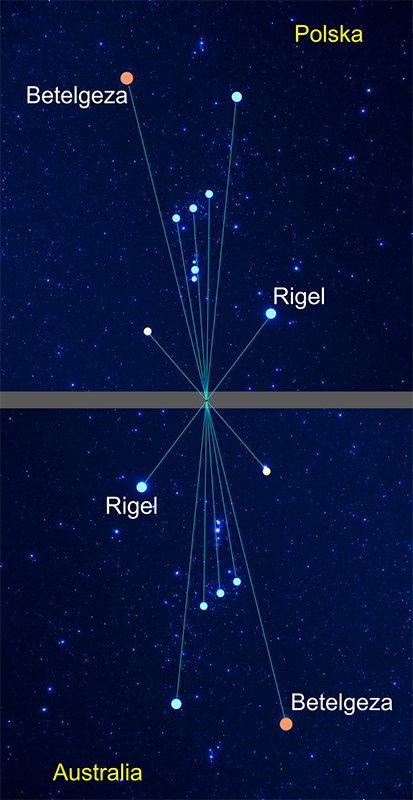
Trzeci przykład dotyczy już samego Oriona, którego w animacji reprezentuje 7 charakterystycznych gwiazd plus mgławica M42 (w różnych kolorach dla lepszego obrazowania).
W animacji przemieszczamy się pomiędzy Polską a Australią z kamerą ustawioną na Oriona i obrotem o 180° po minięciu równika.
We wszystkich trzech przykładach mieliśmy to samo przekształcenie - obrót o 180°. Grafika po prawej w punkcie a) pokazuje taki obrót - wszystko się zgadza: P jest "do góry nogami". a wybrzuszenie, które było "na górze w prawo" jest po obrocie "na dole w lewo".
Obrót jest graficznie trudnym przekształceniem, ale jest inne, tożsame przekształcenie dające ten sam obraz - to symetria środkowa względem punktu (pokazują to rysunki b) i c)).
Tak więc obrót o 180° lub inaczej symetria środkowa, odpowiadają za "różne" obrazy tych samych gwiazdozbiorów oglądanych z półkuli północnej i południowej. Musimy tu dodać, że lekko "naciągamy" sytuację, gdyż nie chodzi o to, aby jednocześnie patrzeć z obu półkul na ten sam gwiazdozbiór, co było by trudne lub często niemożliwe - np. kiedy w Polsce oglądamy na wieczornym, styczniowym niebie Oriona, to w Sydney jest świt i nie tylko, że prawie nie widać już gwiazd, to i tak Orion zaszedł kilka godzin wcześniej. Chodzi o to, aby porównywać ten sam gwiazdozbiór widziany z obu półkul w "tej samej pozycji", czyli np. w sytuacji, gdy linia łącząca dwie wybrane gwiazdy gwiazdozbioru była w obu widokach pionowa i nie jest ważne, że pomiędzy taką sytuacją jest kilka czy kilkanaście godzin różnicy.
Zadanie 1 - Moje niebo
Zadanie dla każdego! Trzeba połączyć wybrane gwiazdy w wyimaginowane gwiazdozbiory wraz z wymyśloną dla nich nazwą (w programie graficznym lub lub na wydrukowanej kartce).
Przykład po prawej pokazuje jaki potencjał twórczy przynosi takie ćwiczenie.
Obrazek z samym gwiaździstym niebem możesz pobrać TUTAJ (.pdf) lub TUTAJ (.jpg)
Zadanie 2 - Odbijamy w symetrii
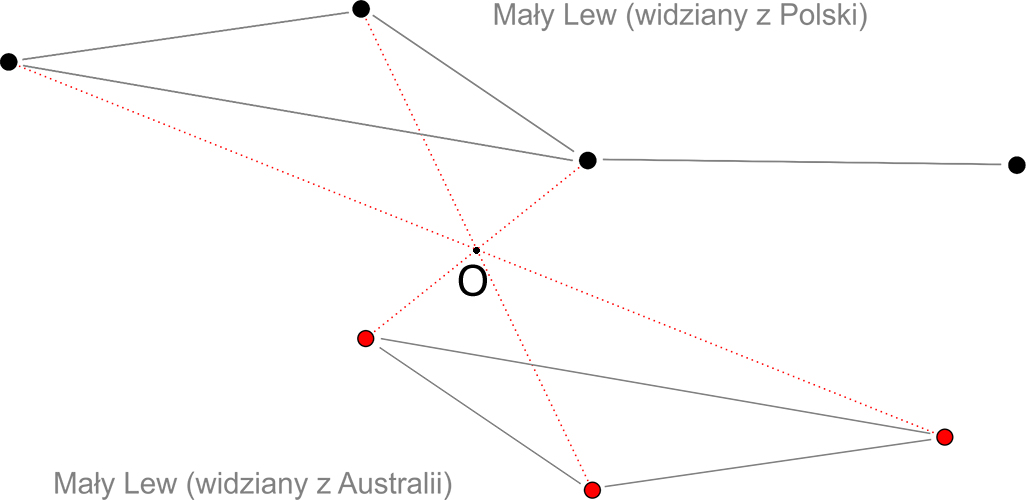
Główne matematyczne ćwiczenie tego tematu. Przygotowany pdf zawiera kilka gwiazdozbiorów, które widać z obu półkul. Rysunki przedstawiają ich widok z Polski, a zadanie polega na narysowaniu ich widoku z Sydney.
Przykład po prawej pokazuje początek tworzenia takiego obrazu przy wykorzystaniu symetrii środkowej - punkt O wybieramy sobie sami i musimy pamiętać, że od O do gwiazdy "z Polski" musi być taka sama długość, jak od O do gwiazdy "z Sydney".
Ciekawostką jest fakt, że rysunki takie wykonują również uczniowie, którzy "nigdy wcześniej nie słyszeli o takiej symetrii.
Przygotowane gwiazdozbiory (po dwa na stronę) można pobrać TUTAJ (.pdf)
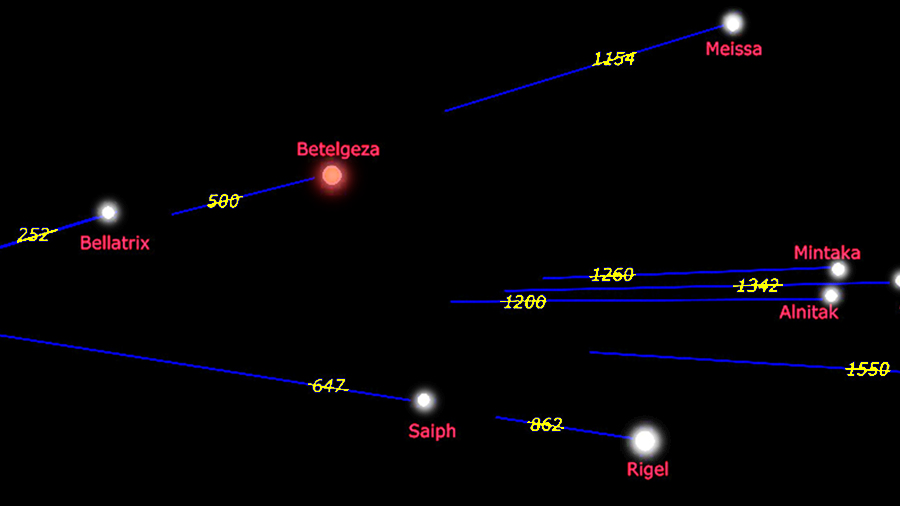
Zadanie 3 - Widziane z boku (na 6)
Grafika po prawej to fragment widoku "z boku" gwiazdozbioru Oriona z podanymi odległościami od Ziemi w latach świetlnych (dla przypomnienia jak to wygląda w przesuwanej animacji: - LINK )
Wersja łatwiejsza
Wybierz jakiś gwiazdozbiór i stwórz jego widok "z boku" (w programie graficznym lub na papierze). Widok taki powinien dotyczyć najbardziej charakterystycznych gwiazd tego gwiazdozbioru i zachowywać zarówno skalę odległości, jak i orientacyjne wzajemne położenie gwiazd widzianych "z boku".
Wszelkie dane do takiego zadania znajdziesz na mapie nieba online (jedna z nich opisana jest poniżej).
Wersja trudniejsza
Takie samo zadanie jak wyżej, tylko efekt ma być w postaci animacji (kamera patrząca z Ziemi na nasz gwiazdozbiór wędruje przez kosmos "patrząc" na niego, aż w końcu zobaczymy go "z boku"). Taka animacja mogła by być stworzona zarówno w jakimś języku programowania, jak i w postaci video z programów do grafiki 3D.
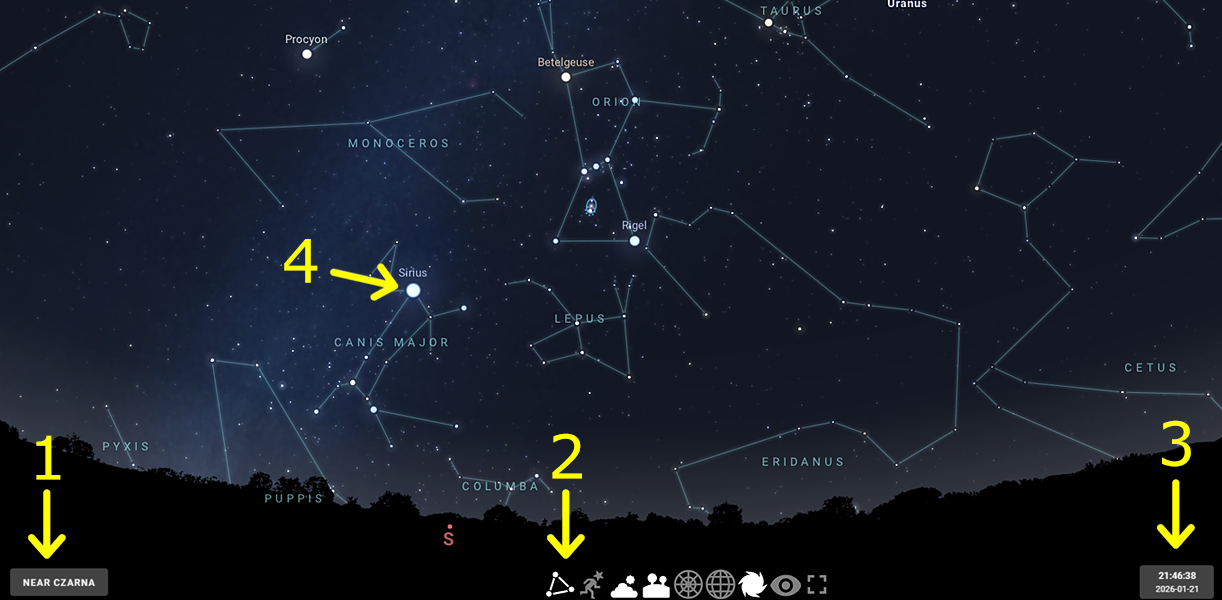
Zadanie 4 - Gdzie jest południe?
Po prawej ekran z bezcennego źródła interaktywnej wiedzy o nocnym niebie - Stellarium - darmowy numer 1 na świecie jeśli chodzi o mapy nieba.
Cztery najważniejsze przyciski to:
1 - ustawenie lokalizacji (z jakiego miejsca na Ziemi patrzymy w niebo),
2 - włączenie/wyłączenie linii gwiazdozbiorów,
3 - ustawienie czasu obserwacji,
4 - po kliknięciu na dany obiekt otrzymamy informacje o nim (w tym odległość w latach świetlnych).
Resztę można odkryć samemu.
Mapa nieba Stellarium Web (online) jest TUTAJ
Program Stellarium do pobrania i zainstalowania jest TUTAJ
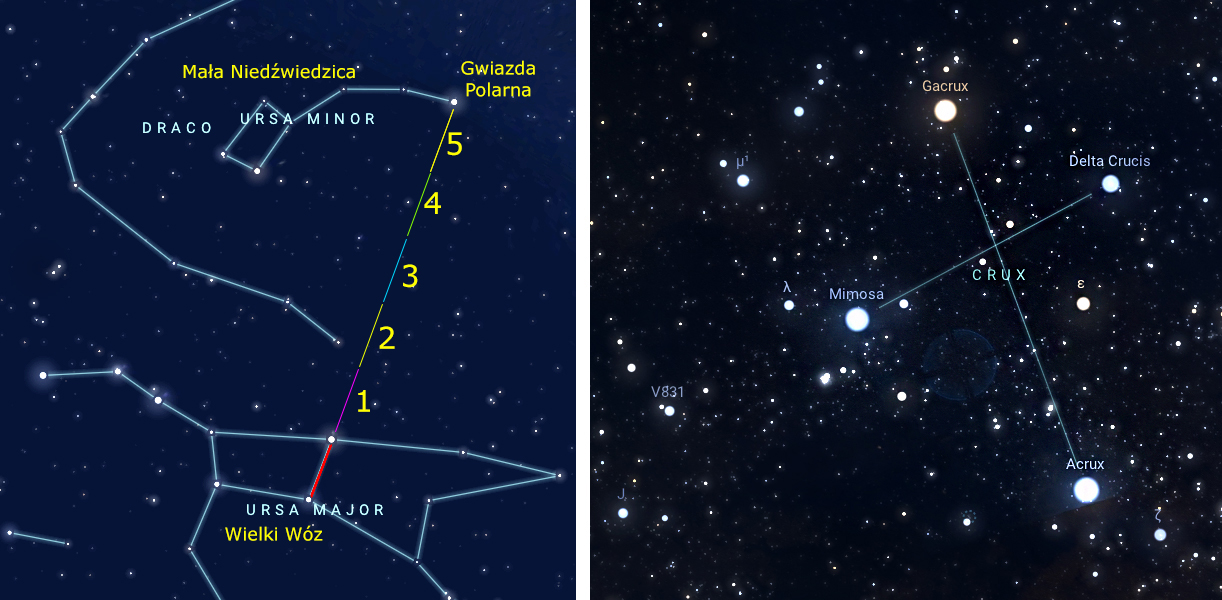
Jednym ze sposobów wyznaczenia kierunku północnego na naszej półkuli jest znalezienie Gwiazdy Polarnej - pierwszy obrazek po prawej przypomina jak to zrobić: po łatwym odnalezieniu Wielkiego Wozu przedłużamy 5 razy odległość pomiędzy jego tylnymi "kołami" (u nas czerwony odcinek) i trafiamy na Gwiazdę Polarną będącą "na końcu" Małego Wozu (tak naprawdę Małej Niedźwiedzicy).
Ale Gwiazdy Polarnej nie widać z półkuli południowej i trzeba tam sięgnąć po inny gwiazdozbiór, aby wyznaczyć kierunek południowy. Jest nim Krzyż Południa (drugi obrazek po prawej).
Zadanie brzmi: Dowiedz się jak za pomocą Krzyża Południa wyznaczyć kierunek południowy i sprawdź to w programie Stellarium.
