

Zadania, w których dokładamy lub usuwamy fragmenty brył należą do trudnych lub bardzo trudnych. Dlaczego? Często usuwane fragmenty są wewnątrz brył i wtedy żaden rysunek czy animacja 3D nie pomoże - trzeba sobie samemu wyobrazić jak to tam wygląda. Są to zadania, przy których wyobraźnia przestrzenna musi pracować na 100% mocy.
Pytania w typowych treściach takich zadań dotyczą najczęściej podania objętości lub, co jest zawsze trudniejsze, pola powierzchni całkowitej takiej "nowej" bryły.
Przykład #6:
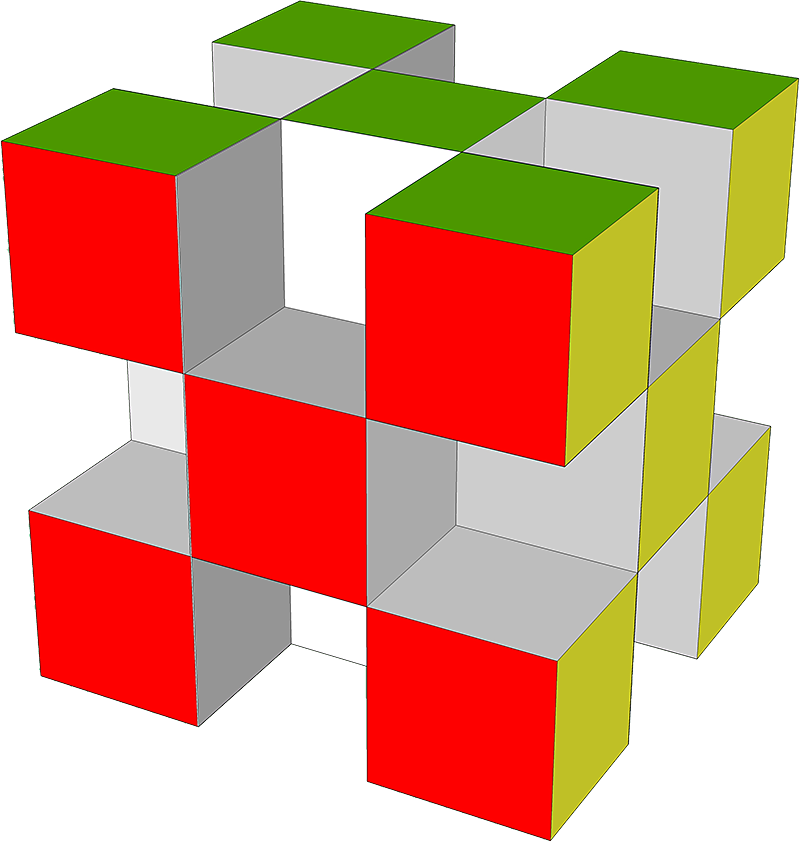
W sześcianie 3cm x 3 cm x 3cm (podobnym do kostki Rubika), usunięto kostkę 1 cm3 ze środka każdej krawędzi (zobacz rysunek).
Oblicz objętość i pole powierzchni całkowitej tej "nowej" bryły.
Aby móc sobie to lepiej wyobrazić, zobacz poniżej jak to wyglada w interaktywnym 3D - obracaj, przybliżaj, a prawym klawiszem myszki przesuwaj (wszystkie klocki są w jednym kolorze aby nie rozpraszać mózgu, wystające odcinki pozwolą na lepszą orientację przy obrotach bryły, a lekkie odstępy pomiędzy kostkami pozwolą lepiej widzieć 3D).
Przesuwaj suwakiem pod bryłą aby "usuwać kostki".
Podane niżej wyjaśnienia sprawdziły się wśród uczniów ze słabą wyobraźnią 3D i są chyba najlepszą metodą w rozwiązywaniu tego typu zadań.
Po usunięciu kostki ze środka krawędzi, powstaje "wnęka" mająca 4 ścianki (kwadraty po 1 cm2), przy czym jak pokazują to rysunki po prawej, dwa z tych kwadratów to kwadraty ze ścian bocznych (czerwony i zielony) "przesunięte równolegle do wnęki".
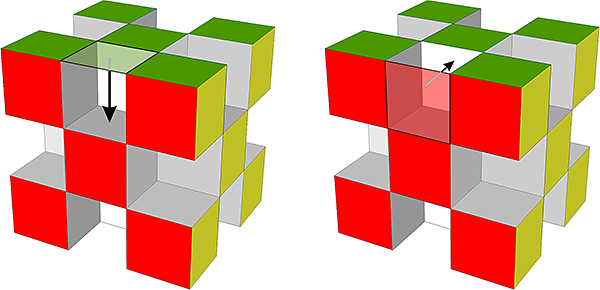
Z 4 kwadratów "we wnęce" zostają więc dwa jako nowe (na rysunku pokazane strzałkami i zaznaczone na czarno). Problem z nimi jest taki, że są we "wnęce" dwóch sąsiednich ścian dużego sześcianu (u nas - zielonej i czerwonej), co oznacza ryzyko dwukrotnego (błędnego) policzenia ich pól zarówno dla ściany czerwonej, jak i zielonej.
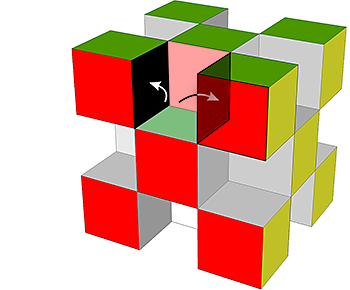
Obliczamy objętość "nowej" bryły: od objętości całego sześcianu 3x3x3 cm (27 cm3) odejmiemy objętość wszystkich "wnęk" (czarne obszary na rysunku: 4 "na górze", 4 "w środku" i 4 "na dole", razem 12), czyli 12•1 cm3 = 12 cm3.
27 cm3 - 12 cm3 = 15 cm3 (objętość "nowej" bryły wynosi 15 cm3)
Przy obliczaniu pola powierzchni całkowitej jest jak się wydaje, najprostszy sposób, który ominie niebezpieczeństwa podwójnego policzenia niektórych kwadratów:
- na każdej ścianie obliczamy pole kolorowych kwadratów, które zostały nie usunięte - w tym zadaniu jest ich po 5 na każdej ścianie: 5•1 cm2 = 5 cm2, czyli dla całej bryły: 6 ścian • 5 cm2 = 30 cm2,
- obliczmy powierzchnię jednej "wnęki" - jest tam 4 kwadraty po 1 cm2 każdy, czyli "wnęka" ma pole `4 cm2
wszystkich "wnęk" jest 12, co daje razem 12 • 4 cm2 = 48 cm2.
Dodajemy pola kolorowych kwadratów do pól "wnęk": 30 cm2 + 48 cm2 = 78 cm2
