Prawa autorskie
  • Wszystkie materiały dostępne na tej stronie internetowej, w tym teksty, grafiki, pliki multimedialne oraz inne treści, są przeznaczone do celów edukacyjnych i podlegają ochronie prawnej.
  • Użytkownicy mają prawo do ich wykorzystywania w ramach nauki – zarówno w szkołach, na lekcjach, jak i w domu. Można je drukować, kopiować i udostępniać uczniom oraz nauczycielom, pod warunkiem, że odbywa się to bezpłatnie i w celach dydaktycznych.
  • Zabrania się jednak ich rozpowszechniania w internecie, sprzedaży oraz wykorzystywania w celach komercyjnych bez uprzedniej, wyraźnej zgody właściciela praw autorskich.
  • W przypadku pytań dotyczących warunków użytkowania prosimy o kontakt.


Polityka prywatności
  • Niniejsza strona internetowa nie zbiera, nie przetwarza ani nie przechowuje żadnych danych osobowych użytkowników.
  • Serwis nie wykorzystuje plików cookies do celów analitycznych, marketingowych ani śledzących. Jedynymi plikami cookies stosowanymi na stronie są te, które są niezbędne do jej prawidłowego funkcjonowania na serwerze, takie jak obsługa sesji użytkownika czy zapewnienie bezpieczeństwa działania witryny.
  • Korzystanie ze strony oznacza akceptację powyższych zasad. W przypadku pytań prosimy o kontakt.

Usunięto/Dołożono

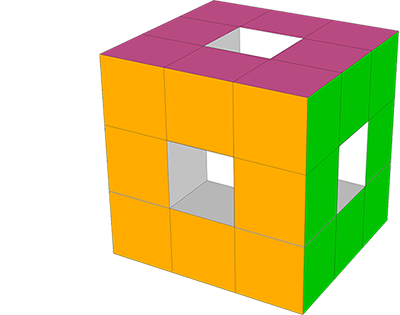
Zadania, w których dokładamy lub usuwamy fragmenty brył należą do trudnych lub bardzo trudnych. Dlaczego? Często usuwane fragmenty są wewnątrz brył i wtedy żaden rysunek czy animacja 3D nie pomoże - trzeba sobie samemu wyobrazić jak to tam wygląda. Są to zadania, przy których wyobraźnia przestrzenna musi pracować na 100% mocy.

Pytania w typowych treściach takich zadań dotyczą najczęściej podania objętości lub, co jest zawsze trudniejsze, pola powierzchni całkowitej takiej "nowej" bryły.



Oto przykład #4:



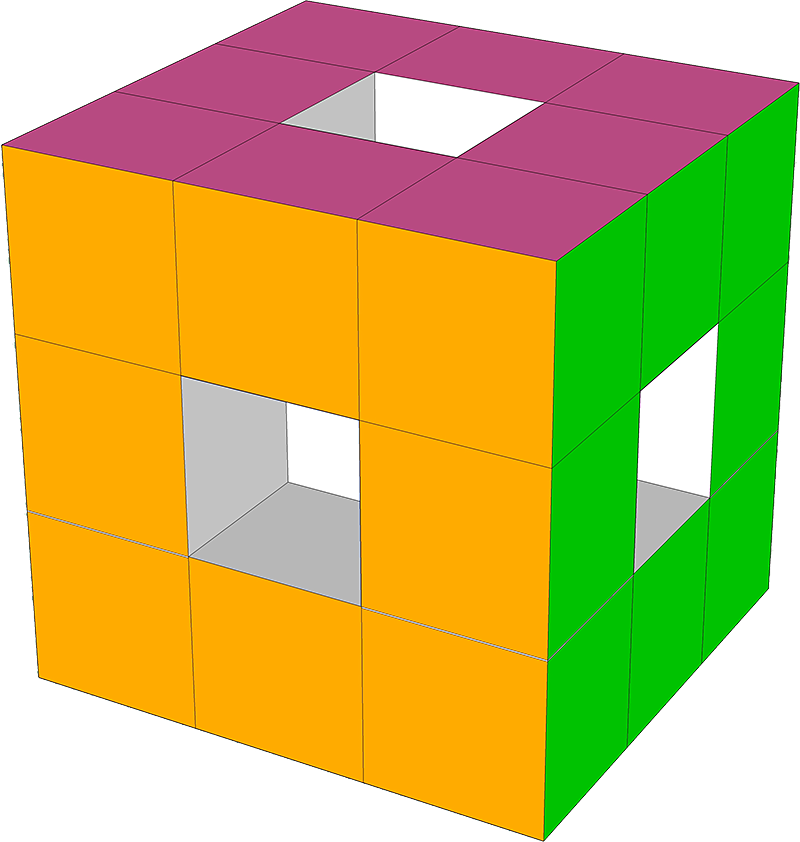
W sześcianie 3cm x 3 cm x 3cm (podobnym do kostki Rubika), usunięto po kostce
1 cm3 ze środka każdej ściany (zobacz rysunek).
Oblicz objętość i pole powierzchni całkowitej tej "nowej" bryły.

Aby móc sobie to lepiej wyobrazić, zobacz poniżej jak to wyglada w interaktywnym 3D - obracaj, przybliżaj, a prawym klawiszem myszki przesuwaj (wszystkie klocki są w jednym kolorze aby nie rozpraszać mózgu, wystające odcinki pozwolą na lepszą orientację przy obrotach bryły, a lekkie odstępy pomiędzy kostkami pozwolą lepiej widzieć 3D).


Przesuwaj suwakiem pod bryłą aby "usuwać kostki".


Jak to rozwiązać?

Podane niżej wyjaśnienia sprawdziły się wśród uczniów ze słabą wyobraźnią 3D i są chyba najlepszą metodą w rozwiązywaniu tego typu zadań.

Usunięto kwadracik, a przybyło 4 nowe

W tym zadaniu, jak w wielu podobnych, obliczenie objętości będzie łatwe, zaś głównym problemem w obliczeniu pola powierzchni całkowitej jest środek ściany, gdzie usunięto kostkę.
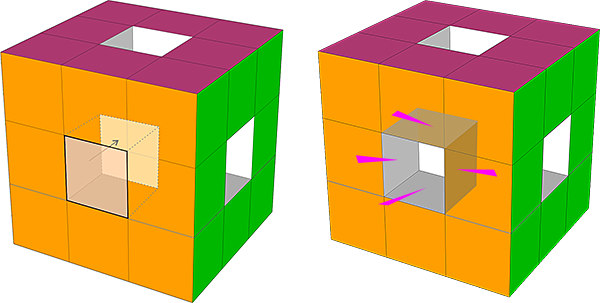
Na widocznym obok rysunku widać, że kwadrat 1 cm2, wprawdzie znika ze ściany sześcianu, ale pojawia się taki sam w głębi (pokazuje to strzałka), a we wnętrzu sześcianu pojawiają się 4 nowe kwadraty (pokazują to różowe strzałki).

Tak więc po usunięciu środkowej kostki, z pola ściany sześcianu nie znika 1 cm2 (przesuwa się w głąb), a dochodzą 4 kwadraty po 1 cm2.

Rozwiązanie

Sześcian miał krawędź 3 cm, więc jego objętość to: V = 3•3•3,
czyli V = 27 cm3
Usunięta ze ściany kostka jest sześcianem o krawędzi 1 cm, więc jej objętość to 1 cm3. Usunięto 6 takich kostek, więc objętość nowej bryły to: 27 cm3 - 6 cm3 = 21 cm3

Pole powierzchni jednej ściany sześcianu to 3•3 = 9 cm2, ale jak było wyjaśnione wyżej, nie tylko nie "znika" 1 cm2, ale przybywa jeszcze 4 cm2, czyli każda ściana nowej bryły ma 13 cm2. Ścian jest 6 więc 6 • 13 cm2 = 78 cm2.