Zadania, w których dokładamy lub usuwamy fragmenty brył należą do trudnych lub bardzo trudnych. Dlaczego? Często usuwane fragmenty są wewnątrz brył i wtedy żaden rysunek czy animacja 3D nie pomoże - trzeba sobie samemu wyobrazić jak to tam wygląda. Są to zadania, przy których wyobraźnia przestrzenna musi pracować na 100% mocy.
Pytania w typowych treściach takich zadań dotyczą najczęściej podania objętości lub, co jest zawsze trudniejsze, pola powierzchni całkowitej takiej "nowej" bryły.
Oto przykład #1:

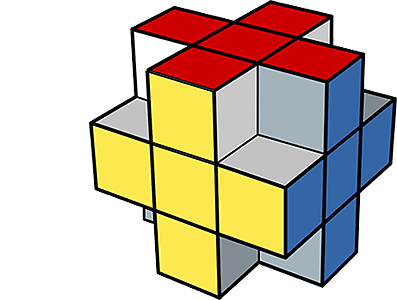
W sześcianie 3cm x 3 cm x 3cm (podobnym do kostki Rubika), usunięto wszystkie narożne kostki (rysunek po lewej pokazuje figurę po usunięciu pierwszej narożnej kostki).
Oblicz objętość i pole powierzchni całkowitej tej "nowej" bryły.
Aby móc sobie to lepiej wyobrazić, zobacz poniżej jak to wyglada w interaktywnym 3D - obracaj, przybliżaj, a prawym klawiszem myszki przesuwaj (wszystkie klocki są w jednym kolorze aby nie rozpraszać mózgu, wystające odcinki pozwolą na lepszą orientację przy obrotach bryły, a lekkie odstępy pomiędzy kostkami pozwolą lepiej widzieć 3D).
Przesuwaj suwakiem pod bryłą aby "usuwać kostki".
Podane niżej wyjaśnienia sprawdziły się wśród uczniów ze słabą wyobraźnią 3D i są chyba najlepszą metodą w rozwiązywaniu tego typu zadań.
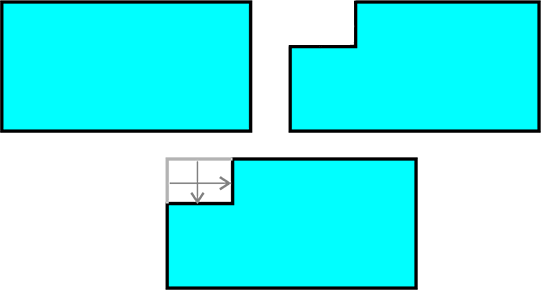
Otworzenie drogi do rozwiązania tego zadania zaczyna się na płaskim prostokącie, z którego usunięto narożny fragment w kształcie prostokąta lub kwadratu.
Pytanie - jak zmienił się obwód tego prostokąta?
Odpowiedź: NIE ZMIENIŁ się!
Rysunek po prawej pokazuje dlaczego - fragmenty z pierwszego obwodu zmieniły jedynie położenie, a więc nowa figura ma taki sam obwód jak pierwotny prostokąt.
Błędne odpowiedzi (że obwód nowej figury jest mniejszy od obwodu prostokąta) biorą się stąd, że nasz mózg bardziej skupia się na polu figury (a to rzeczywiście zmalało).
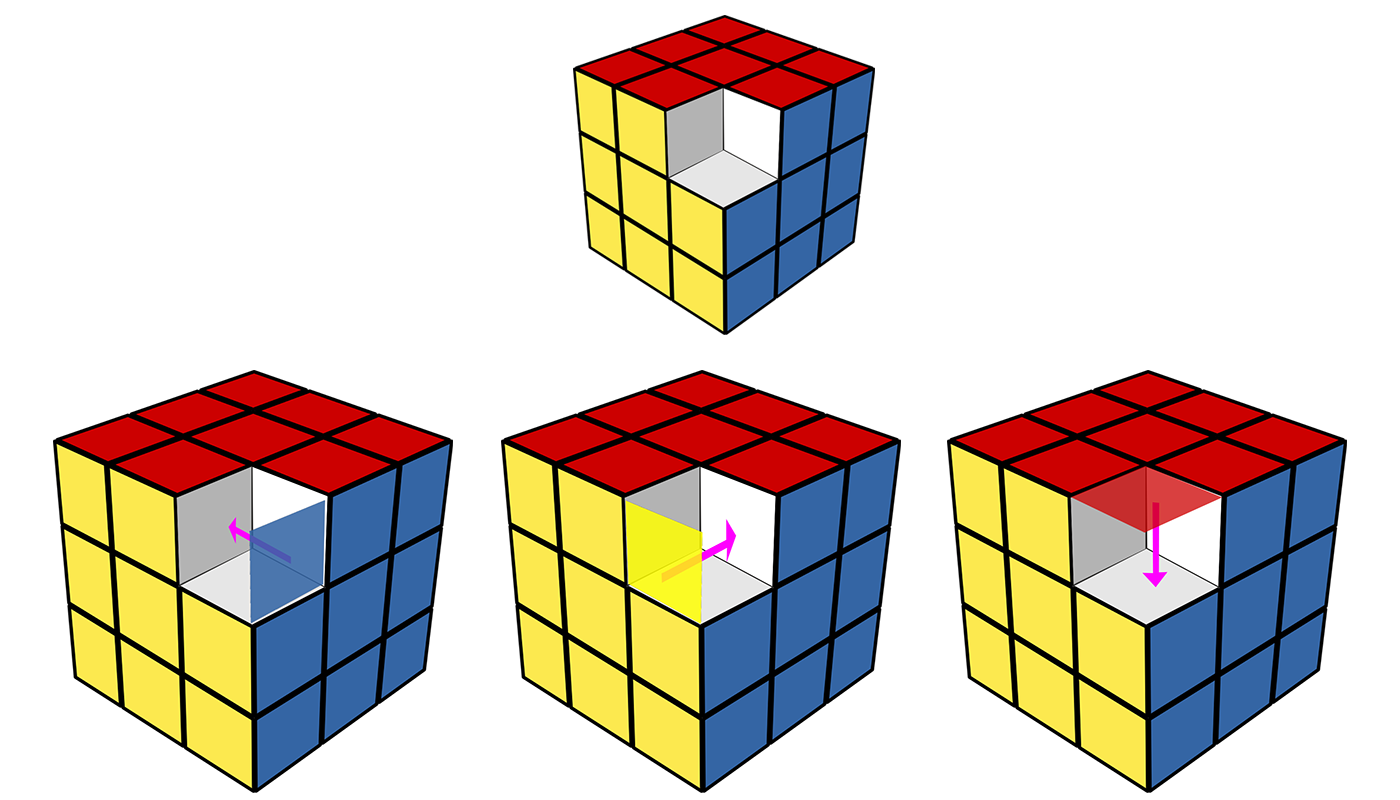
Dokładnie tak samo będzie w świecie 3D - jeżeli z prostopadłościanu lub sześcianu usuniemy narożną kostkę, to oczywiście objętość zmniejszy się, ale pole powierzchni nie!
Widać to na rysunkach, gdzie trzy ścianki "przesuwają się" tylko do nowej bryły i przez to pole powierzchni całkowitej nie zmienia się.
Sześcian miał krawędź 3 cm, więc jego objętość to: V = 3•3•3,
czyli V = 27 cm3
Narożna kostka jest sześcianem o krawędzi 1 cm, więc jej objętość to 1 cm3. Usunięto 8 takich narożnych kostek, więc objętość nowej bryły to: 27 cm3 - 8 cm3 = 19 cm3
Pole powierzchni jednej ściany sześcianu to 3•3 = 9 cm2, więc przy 6 ścianach pole całkowite to 6•9 cm2=54 cm2
Jak pokazano wcześniej, po usunięciu narożnych kostek pole całkowite nie zmienia się, więc pole "nowej" bryły również wynosi 54 cm2.