Te zadania są już bez odpowiedzi; w sam raz na zadanie domowe.

Zadania, które znajdują się poniżej, to jeden z najpopularniejszych typów zadań geometrycznych na świecie (w Polsce można go spotkać na egzaminach ósmoklasistów). Sprawdza przede wszystkim wyobraźnię przestrzenną, przy czym ta sama treść dotyczy ogromnej ilości konkretnych ustawień klocków na rysunku.
Oto to zadanie:
Konstrukcja składa się z takich samych sześciennych klocków o krawędzi 1 cm. Ile trzeba dołożyć takich klocków, aby powstał najmniejszy z możliwych sześcian zawierający w sobie całą tę konstrukcję?
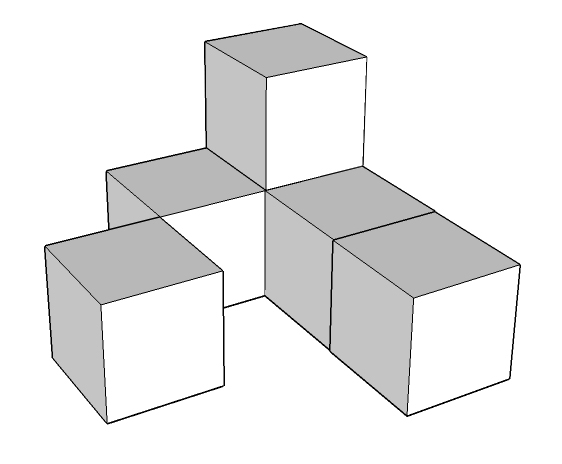
Podane niżej wyjaśnienia sprawdziły się wśród uczniów ze słabą wyobraźnią 3D i są chyba najlepszą metodą w rozwiązywaniu tego typu zadań.
Rysunek obok pokazuje geometryczny efekt końcowy - konstrukcja zostaje obudowana klockami tak, że otrzymujemy sześcian i jest to najmniejszy z możliwych sześcianów zawierający tę konstrukcję.
Bardziej w prawo przykład sześcianu, który też zawiera naszą konstrukcję, ale jest większy (4x4x4x), więc nie spełnia warunków zadania.
Poniżej nasze zadanie w 3D - obracaj (lewy przycisk myszki), przesuwaj (prawy przycisk) przybliżaj (kółko myszki).
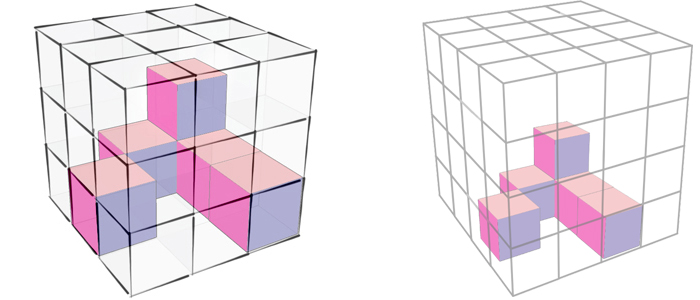
Przesuwaj suwakiem pod bryłą aby "zbudować sześcian".
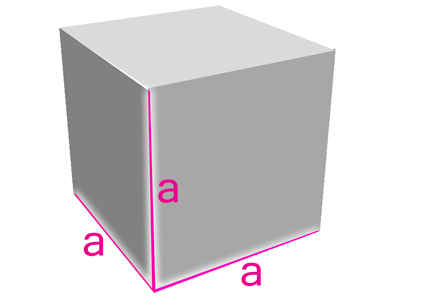
Niby każdy wie, ale ... Sześcian ma 6 takich samych kwadratowych ścian, a dla naszego zadania naistotniejsze jest widzenie trzech takich samych wymiarów pokazanych na sąsiednim rysunku.
To ważne! Klocek nie może wisieć w powietrzu - pod nim aż do podstawy musi być często niewidoczny klocek (klocki).
Nasza konstrukcja ma więc 6 klocków - 5 widocznych i jeden niewidoczny z tej perspektywy.
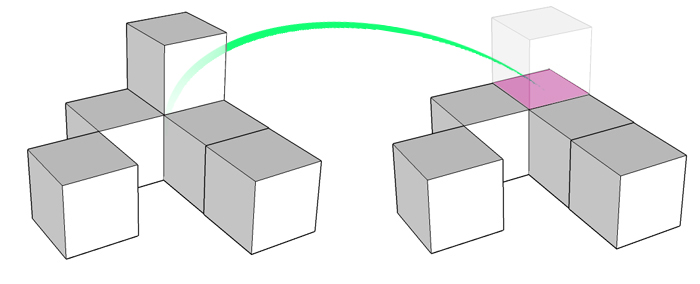
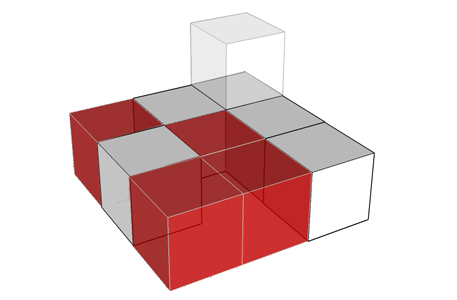
Skupiamy się na najniżej położonych klockach (podstawa konstrukcji) i wyobrażamy sobie (lub szkicujemy) gdzie musimy dołożyć klocki, aby otrzymać kwadratową podstawę. Na rysunku obok są to czerwone klocki.
Mamy więc tymczasową podstawę przyszłego sześcianu o wymiarach 3x3 (tymczasową, gdyż nie sprawdziliśmy jeszcze wysokości i może trzeba będzie tę podstawę powiększyć).
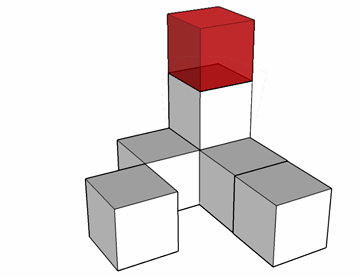
Nasza konstrukcja ma wysokość 2 klocki, więc aby miała taki sam wymiar jak podstawa (3 klocki), to musimy dołożyć jeszcze jeden (czerwony klocek na rysunku).
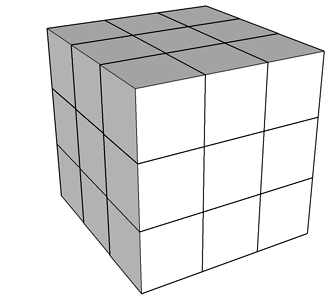
Rysunek pokazuje cały sześcian, który uzupełni naszą konstrukcję - ma wymiary 3x3x3, wieć składa się z 27 klocków.
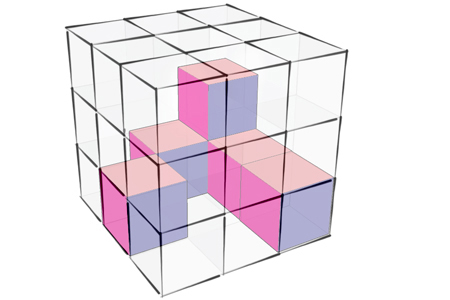
Od ilości klocków całego sześcianu (27) odejmujemy te, które już są w konstrukcji (6):
27 - 6 = 21
Odpowiedź: Do konstrukcji trzeba dołożyć 21 klocków, aby otrzymać najmniejszy z możliwych sześcian, który ją zawiera.
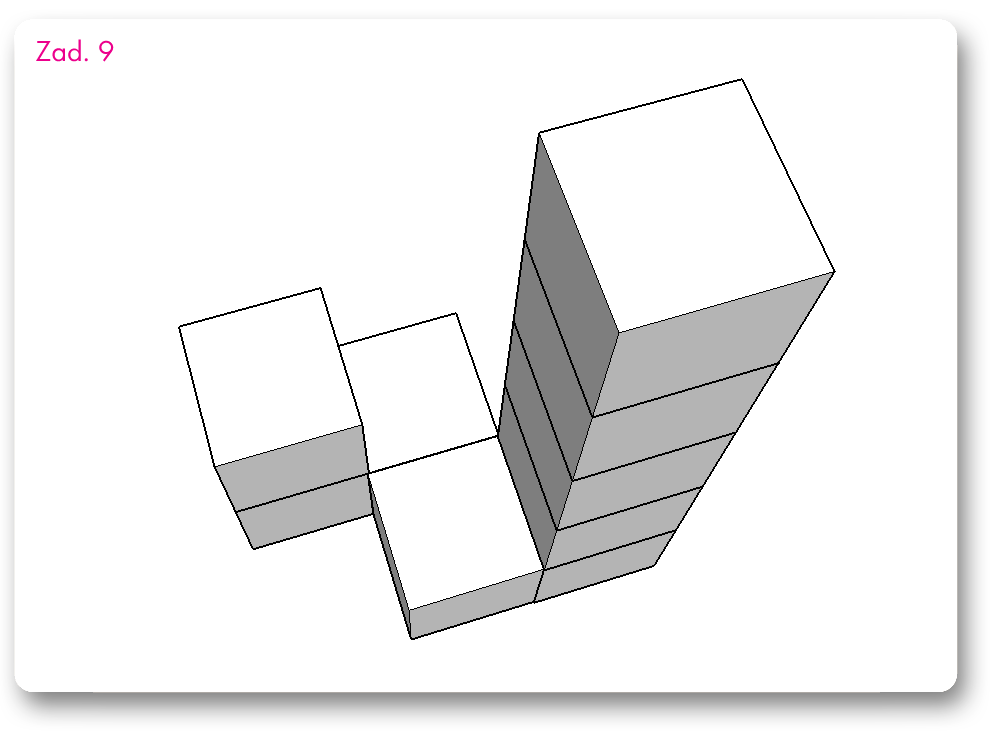
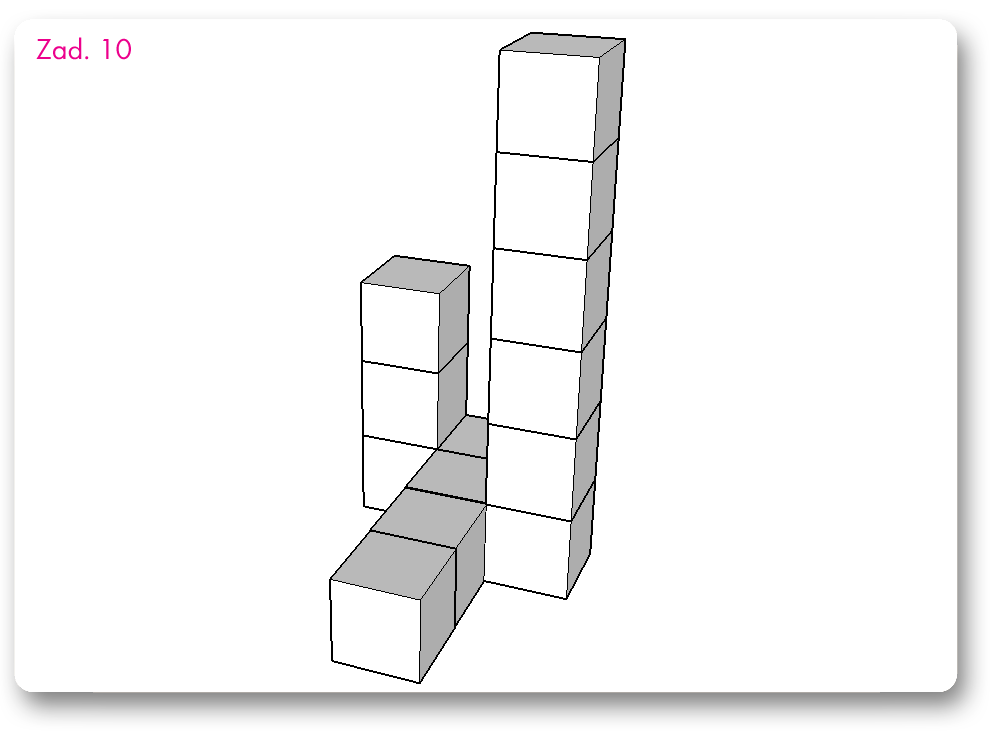
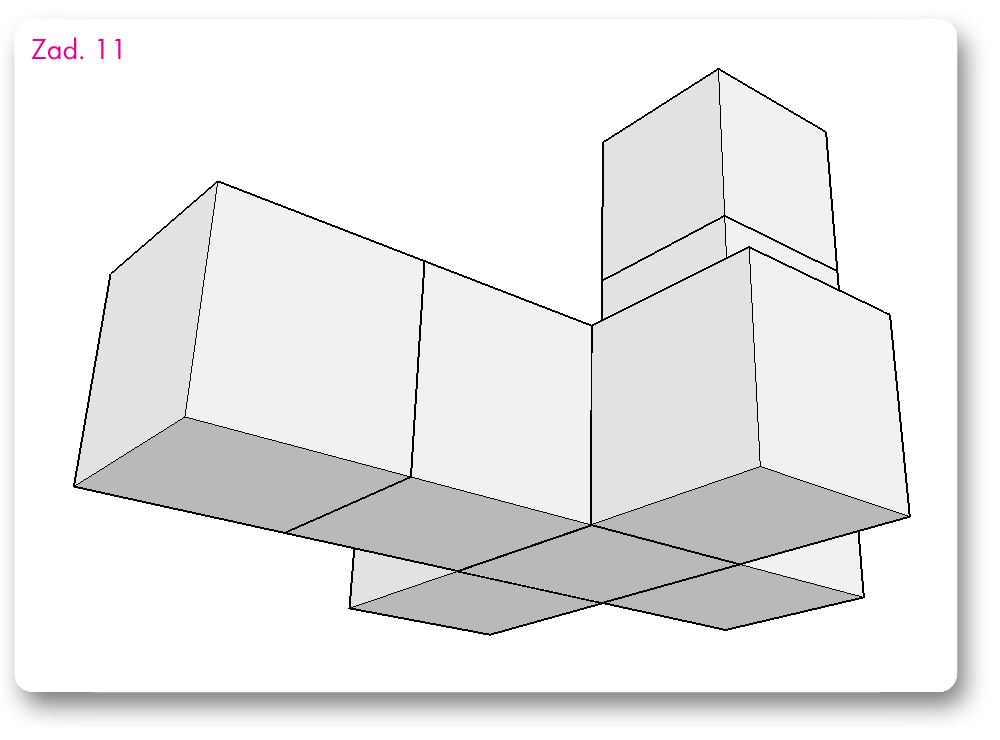
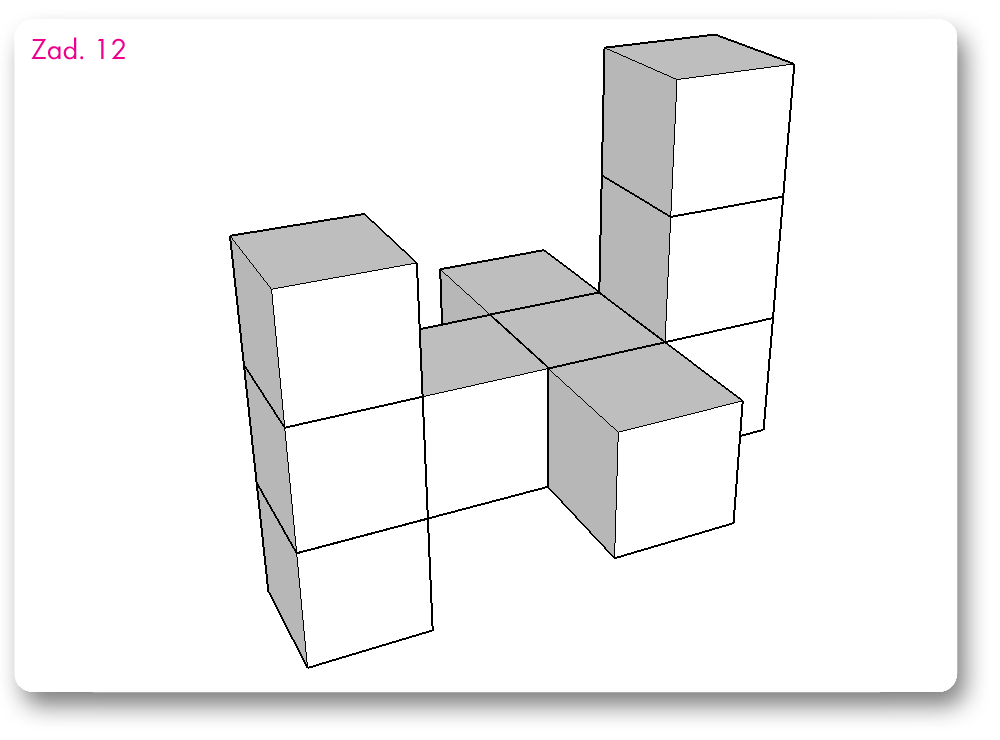
Wszystkie zadania mają taką samą treść:
Konstrukcja składa się z takich samych sześciennych klocków o krawędzi 1 cm. Ile trzeba dołożyć takich klocków, aby powstał najmniejszy z możliwych sześcian zawierający w sobie całą tę konstrukcję?
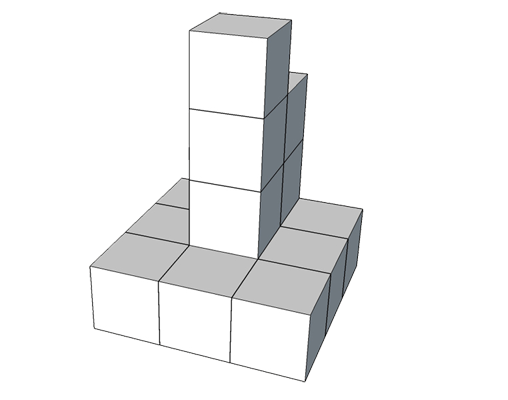
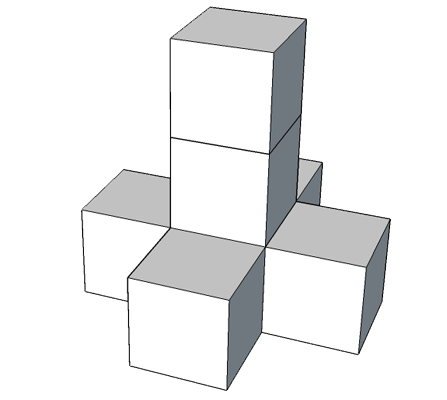
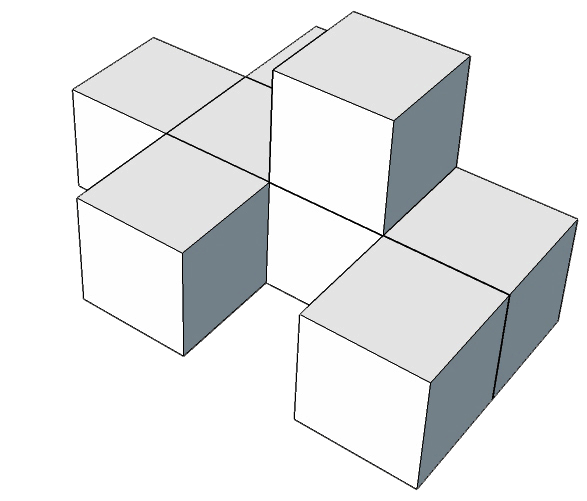
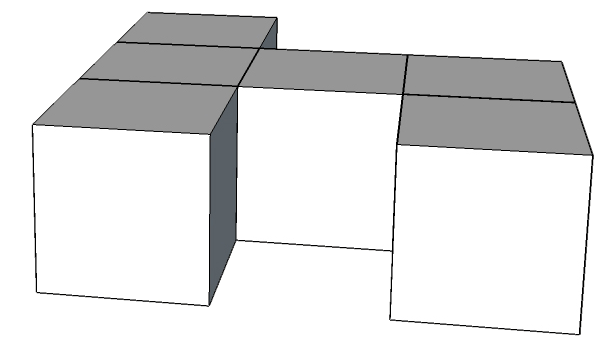
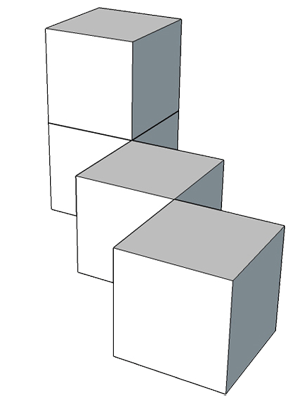
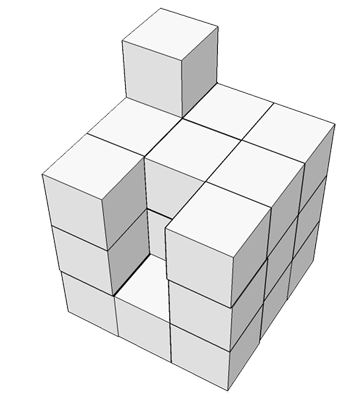
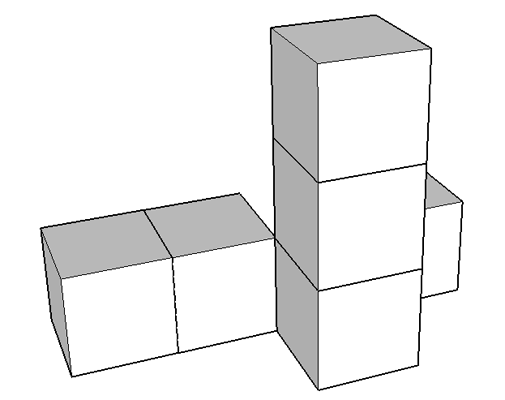
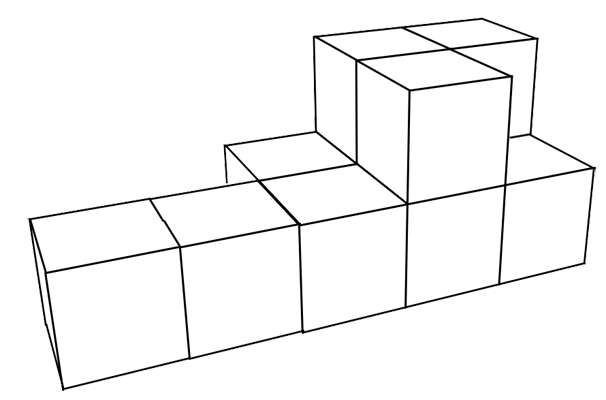
Te zadania są już bez odpowiedzi; w sam raz na zadanie domowe.



