Prawa autorskie
  • Wszystkie materiały dostępne na tej stronie internetowej, w tym teksty, grafiki, pliki multimedialne oraz inne treści, są przeznaczone do celów edukacyjnych i podlegają ochronie prawnej.
  • Użytkownicy mają prawo do ich wykorzystywania w ramach nauki – zarówno w szkołach, na lekcjach, jak i w domu. Można je drukować, kopiować i udostępniać uczniom oraz nauczycielom, pod warunkiem, że odbywa się to bezpłatnie i w celach dydaktycznych.
  • Zabrania się jednak ich rozpowszechniania w internecie, sprzedaży oraz wykorzystywania w celach komercyjnych bez uprzedniej, wyraźnej zgody właściciela praw autorskich.
  • W przypadku pytań dotyczących warunków użytkowania prosimy o kontakt.


Polityka prywatności
  • Niniejsza strona internetowa nie zbiera, nie przetwarza ani nie przechowuje żadnych danych osobowych użytkowników.
  • Serwis nie wykorzystuje plików cookies do celów analitycznych, marketingowych ani śledzących. Jedynymi plikami cookies stosowanymi na stronie są te, które są niezbędne do jej prawidłowego funkcjonowania na serwerze, takie jak obsługa sesji użytkownika czy zapewnienie bezpieczeństwa działania witryny.
  • Korzystanie ze strony oznacza akceptację powyższych zasad. W przypadku pytań prosimy o kontakt.

Sześcian-farba-cięcie-kostki


Jedno z najpopularniejszych na świecie zadań sprawdzających wyobraźnię przestrzenną:



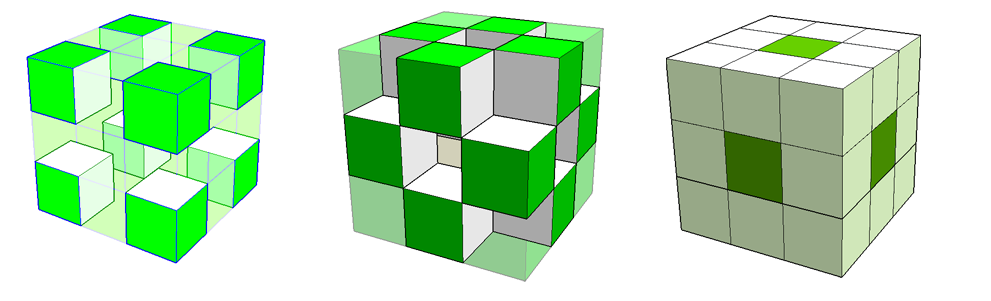
Drewniany sześcian pomalowano na zielono i pocięto tak, jak pokazuje rysunek (3x3x3).
a) Ile z otrzymanych kostek ma trzy zielone ściany?
b) Ile z kostek ma dokładnie dwie zielone ściany?
c) Ile kostek ma dokładnie jedną zieloną ścianę?
d) Ile kostek nie ma ani jednej zielonej ściany?


Trzy pierwsze zadania są "łatwiejsze":
3 zielone ściany - 8 kostek narożnych              2 zielone ściany - 12 kostek              1 zielona ściana - 6 kostek "środkowych"




Największą trudność sprawia policzenie ilości kostek bez zielonych ścian. Z kilku sposobów, jeden wydaje się najlepszy - jest uniwersalny i działa tak samo przy innych kostkach tego typu:

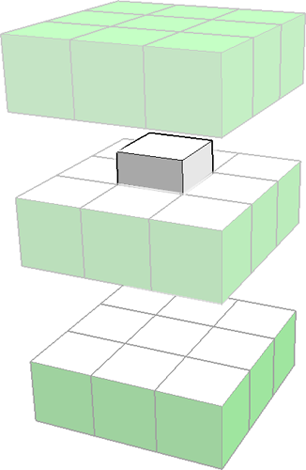
- tniemy sześcian na poziome warstwy o szerokości 1 kostki
(u nas będzie 3 takie warstwy),

- odrzucamy górną i dolną warstwę (tam wszystkie kostki mają coś zielonego),
- "przyglądamy" się pierwszej z pozostawionych warstw (u nas i tak została jedna),

- odrzucamy w niej wszystkie kostki zewnętrzne (brzegowe), gdyż mają zielone ścianki,

- liczymy ilość kostek, które zostały - u nas tylko jedna.


Tak więc w takim sześcianie 3x3x3 jest tylko 1 kostka bez śladu zielonej farby.





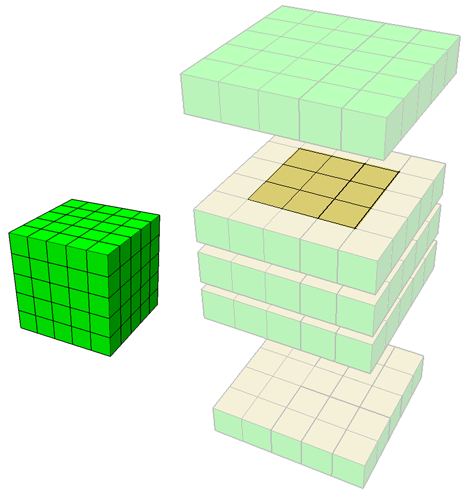Uniwersalność tego sposobu widać jeszcze lepiej na "większych" sześcianach - tutaj 5x5x5:

- tniemy sześcian na poziome warstwy o szerokości 1 kostki
(u nas będzie 5 takich warstw),

- odrzucamy górną i dolną warstwę (tam wszystkie kostki mają coś zielonego),
- "przyglądamy" się pierwszej z pozostawionych warstw,

- odrzucamy w niej wszystkie kostki zewnętrzne (brzegowe), gdyż mają zielone ścianki,

- liczymy ilość kostek, które zostały - u nas 9,

- są 3 takie warstwy, więc 3 · 9=27.


Tak więc w sześcianie 5x5x5 jest 27 kostek bez śladu zielonej farby.





Poniżej kilka sześcianów do ćwiczeń i zadań

Sześcian 4x4x4

Sześcian 6x6x6

Sześcian 7x7x7

Sześcian 9x9x9

Sześcian 10x10x10



A może by tak bez obrazów kostek? Jeśli przyglądniesz się otrzymywanym wynikom, to zauważysz, że nie są to jakieś przypadkowe liczby! Istnieje zależność pomiędzy ilością kostek na krawędzi dużej kostki, a ilością środkowych kostek bez farby; każdy może ją odkryć - Ty też!