Prawa autorskie
  • Wszystkie materiały dostępne na tej stronie internetowej, w tym teksty, grafiki, pliki multimedialne oraz inne treści, są przeznaczone do celów edukacyjnych i podlegają ochronie prawnej.
  • Użytkownicy mają prawo do ich wykorzystywania w ramach nauki – zarówno w szkołach, na lekcjach, jak i w domu. Można je drukować, kopiować i udostępniać uczniom oraz nauczycielom, pod warunkiem, że odbywa się to bezpłatnie i w celach dydaktycznych.
  • Zabrania się jednak ich rozpowszechniania w internecie, sprzedaży oraz wykorzystywania w celach komercyjnych bez uprzedniej, wyraźnej zgody właściciela praw autorskich.
  • W przypadku pytań dotyczących warunków użytkowania prosimy o kontakt.


Polityka prywatności
  • Niniejsza strona internetowa nie zbiera, nie przetwarza ani nie przechowuje żadnych danych osobowych użytkowników.
  • Serwis nie wykorzystuje plików cookies do celów analitycznych, marketingowych ani śledzących. Jedynymi plikami cookies stosowanymi na stronie są te, które są niezbędne do jej prawidłowego funkcjonowania na serwerze, takie jak obsługa sesji użytkownika czy zapewnienie bezpieczeństwa działania witryny.
  • Korzystanie ze strony oznacza akceptację powyższych zasad. W przypadku pytań prosimy o kontakt.


Temat na konkurs matematyczny

Szukasz ciekawego tematu na konkurs matematyczny?

Życie pokazało, że podany niżej temat przyciąga do konkursu bardzo wielu uczniów, łącznie z tymi, którzy na hasło "matematyka" czują "ucisk w brzuchu".
Żadnych "rachunków", trochę kreatywnego działania i zaskakujące rozwiązanie (dla tych, którzy do niego dojdą).



O co chodzi?

Wyobraź sobie, że na oponie koła rowerowego mocujemy jakieś światełko, a nocą filmujemy jazdę takiego roweru.
Na filmie zobaczymy wówczas ślad, jaki w powietrzu zostawia światełko umieszczone na kole roweru.



Ślad

Aby na zdjęciu otrzymać taki ślad stosuje się metodę długiego naświetlania lub składa się go z wielu pojedynczych zdjęć - w obu przypadkach aparat musi być cały czas w stałej pozycji.

Po prawej link do filmiku pokazującego gotowy efekt opisanych wyżej działań.



Cykloida

Linia krzywa, którą było widać na filmiku nosi swoją matematyczną nazwę - cykloida.

Widoczna obok animacja jeszcze raz pokazuje, jak powstaje cykloida.



Zmieniamy tor

A jak wyglądałaby cykloida, gdyby nasze kółko ze światełkiem toczyło się nie po płaskiej drodze, ale wewnątrz okręgu (pierścienia, walca)?






Zadanie konkursowe byłoby takie:

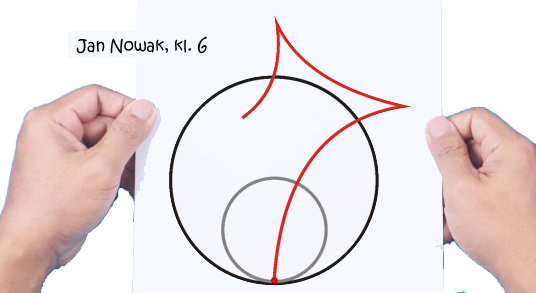
Wewnątrz dużego okręgu (pierścienia, walca) toczy się bez poślizgu koło ze światełkiem, przy czym jest o połowę mniejsze od dużego. Wyjaśnia to poniższy rysunek - jeśli duży okrąg ma 10 cm średnicy, to małe koło ma średnicę 5 cm.




Pytanie brzmi: Jaki ślad zostawi światełko w takim ruchu?


Wydaje się, że najlepszą formą podawania rozwiązań są podpisane kartki z rysunkiem obu okręgów i śladem, jaki według uczestnika zostawi światełko w czasie jednego pełnego okrążenia (zobacz poniższy przykład).



Rady i wskazówki
Trudno jest rozwiązać takie zadanie "w pamięci" i najlepiej jest podjąć konkretne działania ułatwiające rozwiązanie. Można wykorzystać "gotowe" elementy tak, jak pokazują poniższe zdjęcia (jakieś obręcze, bransolety, uszczelki, itp)



albo samemu przygotować prosty zestaw z tektury.




Problem z zadania ma już kilkaset lat (zajmował się nim m.in. Mikołaj Kopernik), a jego rozwiązanie jest zaskakujące i na "początek trudne do przyjęcia".